Kinky Physics: Animating Sine-Gordon Solitons
Recently in one of my classes, we studied the Sine-Gordon theory, which is characterized by the following Lagrangian density in 2 spacetime dimensions:
\[\mathcal L=\frac12\partial^\mu\partial_\mu\phi-V(\phi)\]
Here \(\phi\) is a scalar field and \(V(\phi)=\alpha(1-\cos\beta\phi)\). This equation can be thought of as the continuum extension of a discrete system consisting of pendula connected at their bases by torsion springs. This theory is interesting because it possesses many of the heuristic properties that we would expect of a system comprising particles and antiparticles. The particle-like solutions are the soliton, or ‘kink’, solutions to the Sine-Gordon equations of motion.
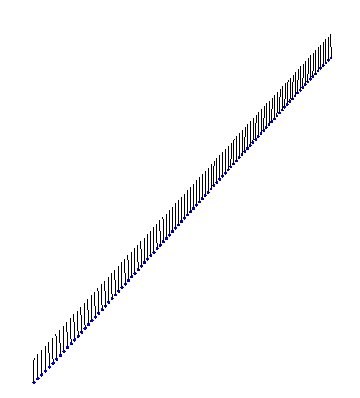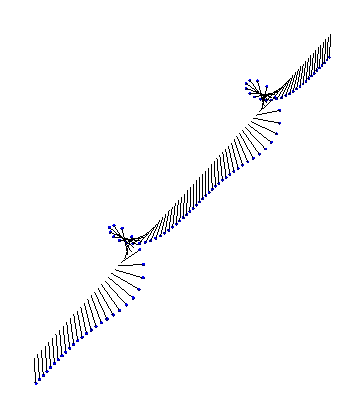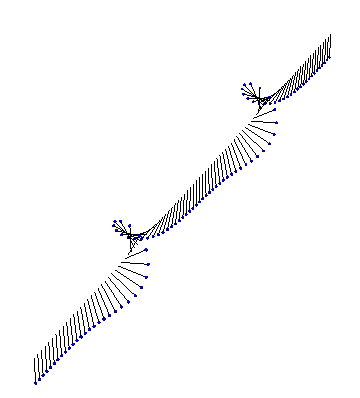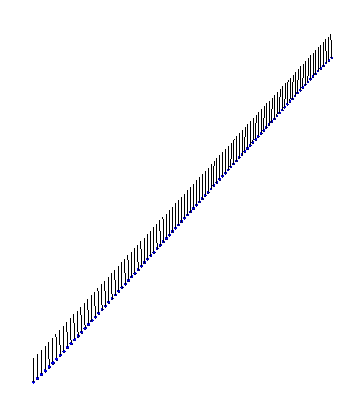
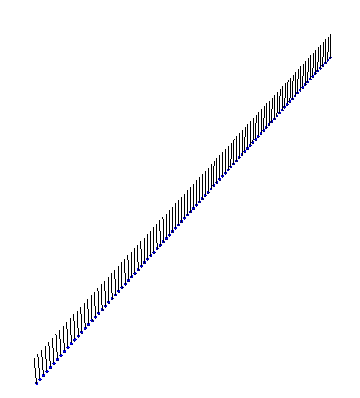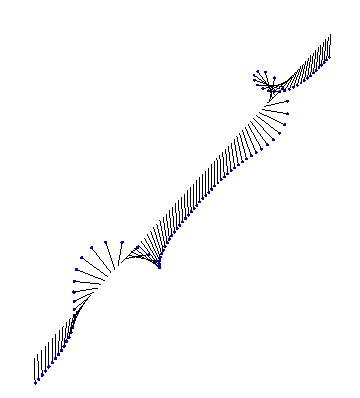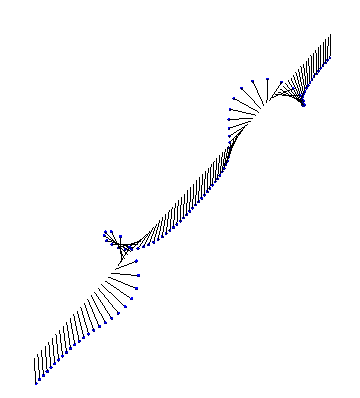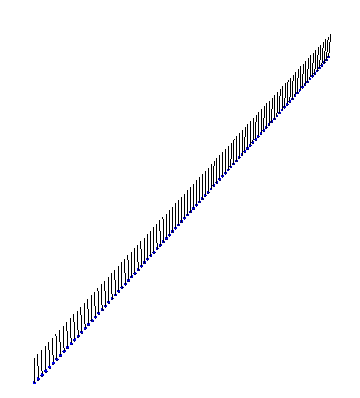
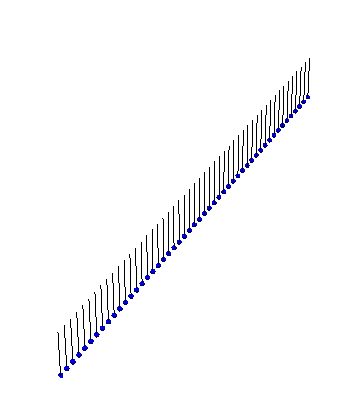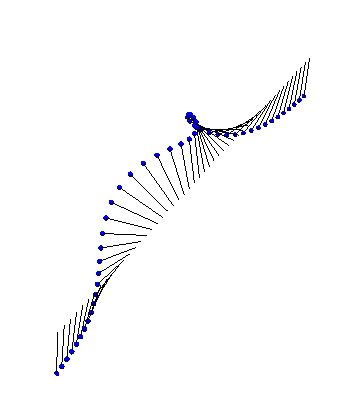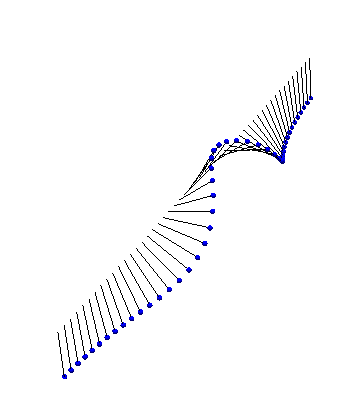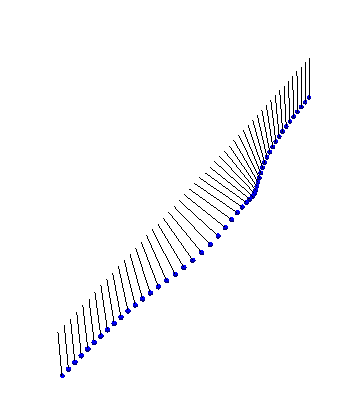
Our instructor couldn’t find a satisfactory video of Sine-Gordon solitons in action, so I whipped up some Mathematica code to visualize the solutions. Here is an example of a kink propagating:
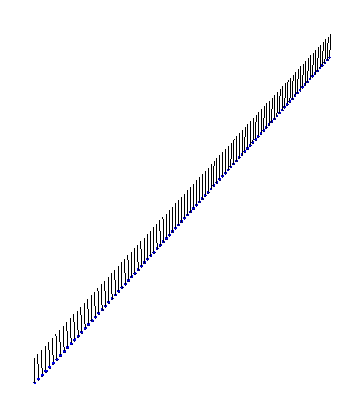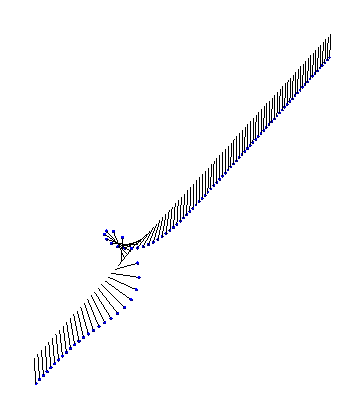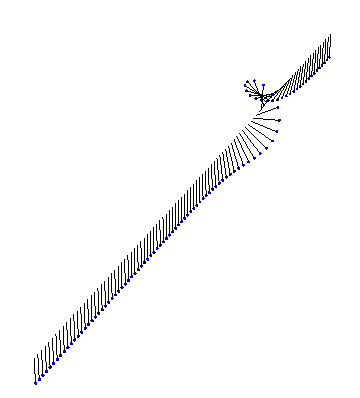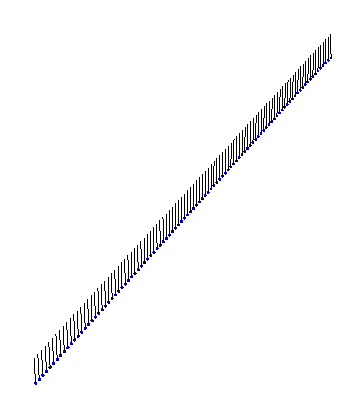 There are also exact analytical forms for arbitrarily many interacting kinks and antikinks. First, we have two kinks colliding and bouncing off each other:
There are also exact analytical forms for arbitrarily many interacting kinks and antikinks. First, we have two kinks colliding and bouncing off each other:
 Next, we have a kink and an antikink collide and propagate through each other:
Next, we have a kink and an antikink collide and propagate through each other:
 Finally, there exists a bound state between a kink and an antikink. This ‘breather’ state looks like:
Finally, there exists a bound state between a kink and an antikink. This ‘breather’ state looks like:
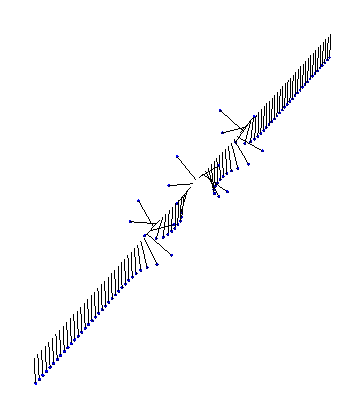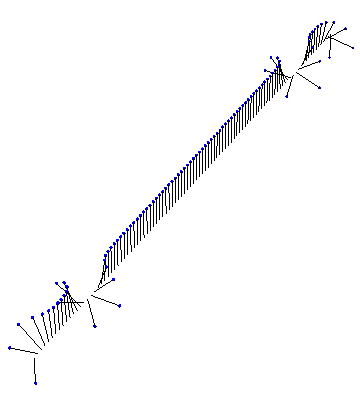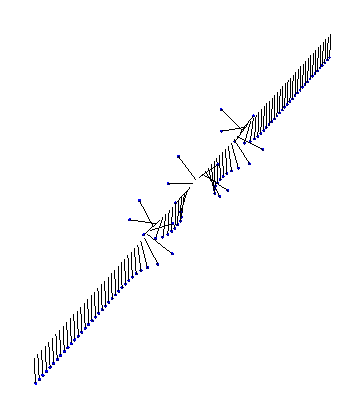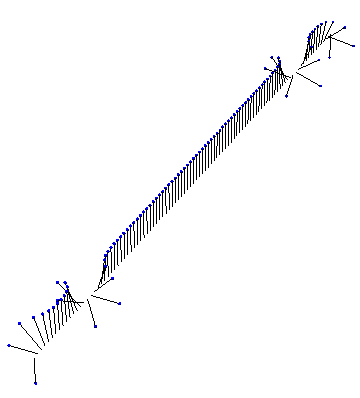
 Of course, we don’t need analytic solutions to visualize something in Mathematica! Here, for instance, is the result of a numeric simulation of a few kinks interacting in fixed boundary conditions:
Of course, we don’t need analytic solutions to visualize something in Mathematica! Here, for instance, is the result of a numeric simulation of a few kinks interacting in fixed boundary conditions:
 If you’d like to play with the Mathematica code, you can download the notebook here. Reading through the code and looking at the examples should be sufficient to understanding how to use it.
If you’d like to play with the Mathematica code, you can download the notebook here. Reading through the code and looking at the examples should be sufficient to understanding how to use it.
 There are also exact analytical forms for arbitrarily many interacting kinks and antikinks. First, we have two kinks colliding and bouncing off each other:
There are also exact analytical forms for arbitrarily many interacting kinks and antikinks. First, we have two kinks colliding and bouncing off each other:
 Next, we have a kink and an antikink collide and propagate through each other:
Next, we have a kink and an antikink collide and propagate through each other:
 Finally, there exists a bound state between a kink and an antikink. This ‘breather’ state looks like:
Finally, there exists a bound state between a kink and an antikink. This ‘breather’ state looks like:
 Of course, we don’t need analytic solutions to visualize something in Mathematica! Here, for instance, is the result of a numeric simulation of a few kinks interacting in fixed boundary conditions:
Of course, we don’t need analytic solutions to visualize something in Mathematica! Here, for instance, is the result of a numeric simulation of a few kinks interacting in fixed boundary conditions:
 If you’d like to play with the Mathematica code, you can download the notebook here. Reading through the code and looking at the examples should be sufficient to understanding how to use it.
If you’d like to play with the Mathematica code, you can download the notebook here. Reading through the code and looking at the examples should be sufficient to understanding how to use it.